蒙特卡罗方法

蒙特卡罗方法（英语：Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

just kidding

这些参数是什么？他们为什么如此重要？

通过统计方法生成的大量数据有时使难以在决策过程中有效使用其结果。正如在有关蒙特卡洛方法的文章中提到的那样，此方法基于“模拟”潜在方案。其在石油和天然气行业中的使用的一个示例是估计潜在生命周期（即资产寿命的可行表示）以预测资产绩效。有时，当运行变化较大的模型时，分析人员会进行超过 1000个生命周期的模拟。该数字乘以模拟资产性能所需的指定期限（即平台使用寿命 = 10-20年）意味着我们正在有效跟踪数万年的模拟。

P10，P50和P90是有用的参数，可用来了解数字在样品中的分布方式。让我们尝试通过一个例子来解释。

考虑以下示例（观察列表）。它们可以代表任何东西-桔子，香蕉，生产效率，CPU使用率等：

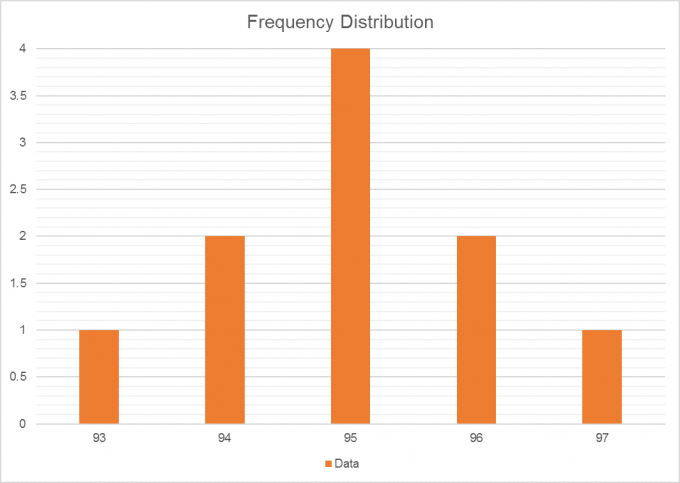
有几个选项可以显示此数据。您可以决定将观察值分组在特定范围内，并创建频率表（即观察值在样本中出现的频率）。这是通过用特定值对观察值进行计数并除以观察总数而得出的（例如，在有十个观察值的样本中，有93次出现一次，因此其出现率为10％）：

数据	数	频率
93	1个	10%
94	2个	20%
95	4个	40%
96	2个	20%
97	1个	10%

该频率还可用于创建著名的“钟形”曲线：

正态分布，即贝尔曲线

通过这种分布，无需访问样本中的所有数据点即可开始推理工作。通过查看图表，我们可以看出大多数观察结果在95左右。

超越和不超越的累积频率和概率是多少？

显示此分布的另一个选项是使用“累积频率”图。该表是通过将频率分布表中的每个频率与其前身的总和相加得出的。人们会注意到，您可以从较低的观察值开始到较高的观察值，或者相反。因此，我们必须引入两个新概念：

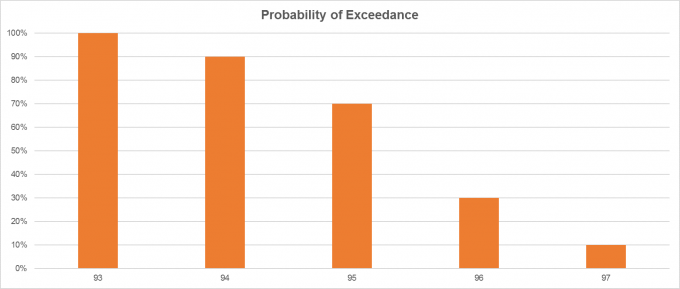
超越概率：如果您从钟形曲线的左侧（即较低的观察值）开始向右（即较高的观察值）开始，则正在建立超越概率的曲线。
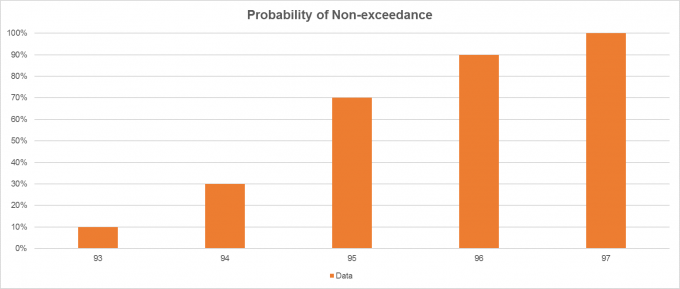
非超标概率：如果您从钟形曲线的右侧（即较高的观察值）开始向左（即较低的观察值）开始，则表示正在建立非超越曲线的概率。

因此，考虑我们的样本，如果我们正在准备一个超越概率图，我们知道数据97的概率出现在10％的频率中，而数据96的概率出现在20％的频率中，因此对于累积频率分布，我们将有数据96的概率与30％的概率相关联。这意味着30％的观测值将超过96的值。

数据	数	频率	超越概率
93	1个	10%	100%
94	2个	20%	90%
95	4个	40%	70%
96	2个	20%	30%
97	1个	10%	10%

超越概率

同样，此图将随着观察值的减小而增加发生的频率，即我们观察值的30％等于超过96的值。这就是所谓的超越概率。

如前所述，另一种选择是相反的看法–增加观察频率，但不会超过观察值。

因此，考虑我们的样本，如果我们准备一个非超越概率图，我们知道93出现在10％的时间，而94出现在20％的时间，因此对于累积频率分布，我们将有数据94的概率与30％的概率相关联。这意味着30％的观测值将等于或不超过94的值。

数据	数	频率	非超越概率
93	1个	10%	10%
94	2个	20%	30%
95	4个	40%	70%
96	2个	20%	90%
97	1个	10%	100%

非超越概率

您还应该注意，对于相同的分布，超越概率的P10(96)与不超越概率的P90(96)完全相同。另一个有用的概念是指这些分布的第一个和最后一个值。超越概率的第一个值和不超越概率的最后一个值将始终等于所有观测值的总数，因为所有频率已经被添加到先前的总数中。同样，在处理大样本时，这种分布可能非常有用。

什么是P10，P50和P90呢？

最后，在P10，P50和P90中，“P”代表百分位数。计算值将取决于您选择创建的分布类型。例如，如果我们决定采用概率超过曲线，则当我们声明某个分布的P10为X时，就是说“在此分布中，有10％的观测值将超过X的值”。

因此，在我们的样本中，P10为96.1 – 10％的观测值将超过96.1的值。P90为93.9 – 90％的我们的观测值将超过93.9的值。

请注意，这并不意味着估算值有90％的机会发生–这是一个非常不同的概念。P50更可能发生，因为它更接近平均值。对于此观察样本，我们的P50为95，恰好是平均值（即95）。这是有原因的，本文稍后将对此进行说明。

通过excel方式计算

对应的不超越概率：
P10 = PERCENTILE(E1:E10,0.1) 93.9
P90 = PERCENTILE(E1:E10,0.9) 96.1

通过python方式计算

1.计算公式

（1）首先将输入的数组进行从小到大排序，然后计算: (n−1)∗p=i+j （其中n为数组元素的个数，将计算结果的整数部分用i表示，小数部分用j来表示，p是百分位数，如90%的话就是0.9）
（2）计算百分位数 res=(1−j)∗array[i]+j∗array[i+1] （res就是我们所需要的百分位数）

2.python代码实现

#!/usr/bin/env python
#coding:utf8

def test_percentile():
    """
    方式一：直接写算法
    :return:
    """
    array = sorted([95, 95, 96, 95, 97, 93, 94, 95, 96, 94])
    """93 94 94 95 95 95 95 96 96 97"""
    n = len(array)
    location_10 = (n - 1) * 0.1
    i = int(location_10)
    j = (round(location_10, 1) - i)
    percentage10 = (1 - j) * array[i] + j * array[i + 1]

    location_50 = (n - 1) * 0.5
    i = int(location_50)
    j = (round(location_50, 1) - i)
    percentage50 = (1 - j) * array[i] + j * array[i + 1]

    location_90 = (n - 1) * 0.9
    i = int(location_90)
    j = (round(location_90, 1) - i)
    percentage90 = (1 - j) * array[i] + j * array[i + 1]
    print(percentage10, percentage50, percentage90)  # 输出：(93.9, 95.0, 96.1)

def test_numpy_percentile():
    """
    方式二：使用numpy库
    :return: None
    """
    import numpy as np
    array = sorted([95, 95, 96, 95, 97, 93, 94, 95, 96, 94])
    percentage10 = np.percentile(array, 10)
    percentage50 = np.percentile(array, 50)
    percentage90 = np.percentile(array, 90)
    print(percentage10, percentage50, percentage90)  # 输出：(93.9, 95.0, 96.1)

if __name__ == "__main__":
    test_percentile()
    test_numpy_percentile()

方差

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。

方差是衡量源数据和期望值相差的度量值。方差越小越稳定。

这种统计方法在我们工作中有什么用？

平时我们有大量的flink job以taskmanager的方式运行在mesos服务器上，每一个taskmanager是一个container，一个flink job会有上百个这样的 taskmanager（container）

当我们有很多个flink job的时候，会有成千上万个taskmanager（container），这时我们就需要对一个flink job的所有taskmanager做一个统计，看看所有taskmanager的CPU使用率情况。

如果我们只使用avg平均值来统计CPU的使用率，这样的误差会很大。

我们使用三个指标来衡量CPU的使用率情况: P50, P90和方差

P50: quantile(0.5, cpu_percent{framework_name=~"$FRAMEWORK_NAME", cluster=~"$CLUSTER"}*100) by (framework_name)
P90: quantile(0.1, cpu_percent{framework_name=~"$FRAMEWORK_NAME", cluster=~"$CLUSTER"}*100) by (framework_name)
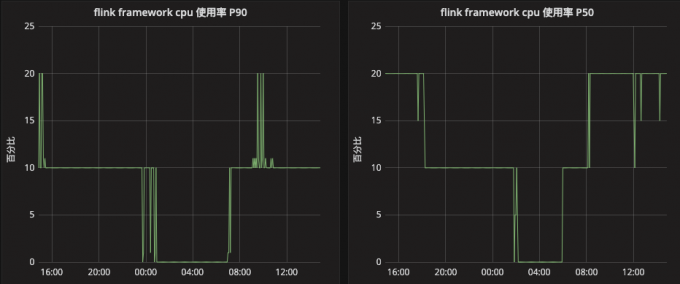
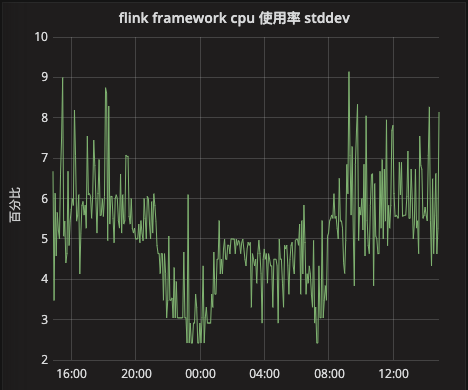
方差: stddev(cpu_percent{framework_name=~"$FRAMEWORK_NAME", cluster=~"$CLUSTER"}*100) by (framework_name)

展示的话可以使用grafana，图形如下：

下图说明90%的taskmanager的CPU使用率最高达到了20

P90 P50

我们认为方差在10以下，偏离度就算比较小的了：

方差

P10，P50，P90和方差

Table of Contents